DESS TSI - Informatique Appliquée à la Mécanique

Première session 2002

Durée : 2h. documents personnels, calculatrice autorisés.

Nous désirons créer un programme (en C) d'analyse de treillis (dans le plan). Un treillis est un assemblage de barres (généralement des profilés rectilignes), assemblées entre elles en des endroits appelés "noeuds". Pour ce sujet, nous allons admettre les hypothèses suivantes :

• systèmes plans (géométrie, chargement et déplacements tous dans le même plan).
• Les barres sont articulées aux noeuds (liaison rotule). En fait, même si c'est rarement le cas (liaison complète soudée, rivée, boulonnée...), les liaisons ne peuvent effectivement pas transmettre un couple du fait du manque de raideur des barres.
• Les charges extérieures sont uniquement appliquées aux noeuds (si un autre chargement est appliqué à une barre, un calcul de statique simple permet d'en trouver l'équivalent, uniquement appliqué aux extrémités, ceci bien sûr après avoir vérifié la résistance de la barre à cette sollicitation).
• Des deux hypothèses précédentes découle le fait que les barres, soumises uniquement à deux forces, ne travaillent qu'en traction/compression. Nous supposerons que les barres en compression ont un profil empêchant le flambage.
• Nous négligerons le poids des barres (et ne pourrons donc pas étudier la tour Eiffel).
• Le système est triangulé et isostatique (soient nbn le nombre de noeuds et nbb le nombre de barres, alors 2*nbn - nbb = 3 )

Si d'autres hypothèses vous semblent nécessaires, faites les (mais justifiez les aussi).

Exemple de treillis : voir figure 1 (fin du sujet, page 3).

Question 1 : Pour représenter en mémoire la géométrie d'un treillis, nous allons déclarer dans notre programme :

#define MaxN 100
#define MaxB (2*MaxN - 3)

typedef struct noeud {float x;float y;int nb;} noeud;
typedef struct barre {int n1;int n2;float lng;} barre;

typedef noeud tabnoeud[MaxN];
typedef barre tabbarre[MaxB];

/* déclarations globales car doivent être accessibles partout */
int nbn,nbb;
tabnoeud tn;
tabbarre tb;

Chaque noeud est identifié par son numéro entre 0 et nbn-1 (contrairement à la figure 1 où il est identifié par une lettre), on connaît ses coordonnées x et y, ainsi que le nombre de barres qui y sont attachées. Chaque barre est identifiée par son numéro (entre 0 et nbb-1), et on connaît les numéros de noeud de ses deux extrémités, ainsi que sa longueur lng. Ecrivez une fonction nommée saisie_geometrie qui demande à l'utilisateur le nombre et les coordonnées des noeuds, puis les numéros des extrémités de chaque barre, puis calcule automatiquement les autres données.

Question 2 : Pour résoudre le système, une méthode est d'écrire toutes les équations d'équilibre aux noeuds (somme des forces = 0), ainsi qu'aux barres (deux forces, donc égales et opposées), et à l'ensemble (force et moment), puis résoudre le système. Nous n'allons pas résoudre le système ici, mais nous (vous, plutôt) allons préparer le calcul, en particulier l'équilibre aux noeuds. En un noeud nous avons en fait deux équations : en X et en Y. Les forces appliquées à ce noeud sont le chargement extérieur (que nous mettons dans le second membre, non traité pour l'instant), et les efforts des barres, tous colinéaires aux barres. Nous allons créer un "premier membre" qui est une matrice de 2*nbn lignes (deux par noeud, une en X et une en Y), et nbb colonnes (une par barre). La première ligne de cette matrice représente l'équation en X de l'équilibre du premier noeud. Elle comportera donc une valeur entre -1 et 1 pour chacune des barres connectées à ce noeud (représentant la proportion de l'intensité de la force projetée sur X, donc le cos de l'angle, positif pour les barres à gauche du noeud, négatif sinon), 0 pour toutes les autres barres. La seconde ligne traite du même noeud, en Y. Les lignes suivantes traitent les autres noeuds, de la même manière.

figure 2 : exemple de ligne

Question 3 : Ecrivez en HTML une page présentant un treillis et ses caractéristiques, d'aspect proche de la feuille ci-après. La figure est stockée dans un fichier nommé "treillis.gif". Le site de Dunod est à l'URL http://www.dunod.fr

Remarques : les questions sont indépendantes. Essayez de répondre au maximum de questions, même sans fignoler les détails. Pensez à expliquer (un peu) ce que vous faites. Pour les questions en C, mieux vaut répondre en partie à la question que pas du tout, par exemple si vous ne savez pas comment on écrit une fonction, donnez au moins les instructions effectuant le calcul demandé, ou si vous ne vous souvenez plus d'un nom en C, mettez le en français. Si vous ne comprenez pas mon organisation des données, vous pouvez à la rigueur m'en proposer une autre.

TREILLIS SPECIAL DESS

ref. pat-25-03-02

Schéma :

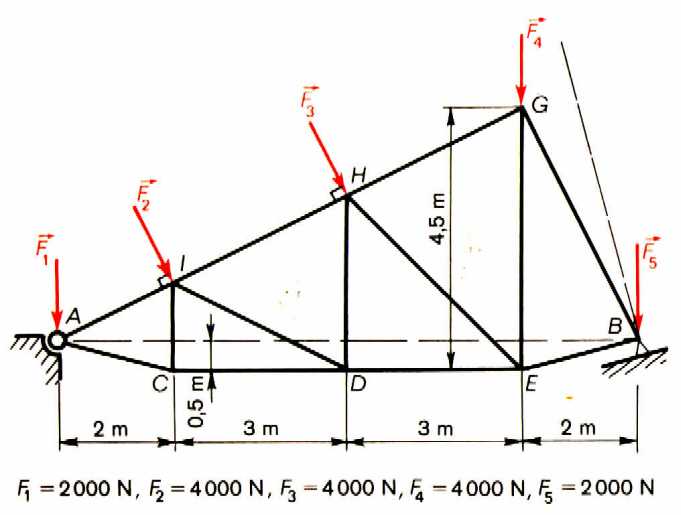
schéma tiré du livre "mécanique 1ères F, tome 1" de Lemasson et Gal (édité chez Dunod).

Caractéristiques :

pour tout renseignement sur ce produit, envoyez un mail à xxxxxx@yyyyyyy.fr.

Pour retourner au sommaire des sujets d'examen, cliquez ici. Mais peut-être aimeriez vous auparavant voir une proposition de correction ?

Patrick TRAU, ULP - IPST avril 02