
Durée : 3h. Cours manuscrits, correction des TP et documents distribués en cours autorisés.
Profitant du calme de cette période suivant Noël, un fabriquant de jouets désire améliorer la conception d'un certain nombre de ses produits. Aujourd'hui, nous allons analyser la stabilité de différents jouets, et en particulier des figurines. Pour qu'une figurine soit stable, il faut que la projection verticale de son centre de gravité se place au plus près du centre de la surface de sustentation (surface convexe englobée par la courbe enveloppe entourant tous les points de contact entre la figurine et le plan horizontal sur lequel elle est posée).
Les questions ci dessous ne tenteront pas de résoudre la globalité du problème, mais chaque partie traitera un point particulier, avec des hypothèses simplificatrices qui ne sont pas les mêmes pour chaque partie. Les trois parties sont donc indépendantes et peuvent être traitées dans l'ordre qui vous convient (et même les questions, à condition de bien les numéroter). Le sujet est long, le barème en tiendra compte (mais il faut aller vite, pas de blabla inutile).
|
Dans un premier temps, il faut décider d'un "modèle", c'est à dire décider comment on représentera la géométrie de la figurine dans notre programme. Nous choisirons de considérer une figurine comme un ensemble de volumes élémentaires. Nous nous limiterons aux figurines composées d'un seul matériau, homogène. On se limitera également à un nombre restreint de volumes élémentaires, mais au moins sphères, cônes, troncs de cônes, cylindres (limités par des plans perpendiculaires à l'axe), parallélépipèdes rectangles. Toute position et orientation de ces volumes élémentaires doit être envisageable, mais on ne traitera pas les figurines articulées. Question 1 : Proposez un modèle. Il doit être assez "souple" pour prendre en compte un maximum de jouets. Vous expliquerez (en français) comment vous organiseriez vos types de données. Vous pouvez également faire de petits schémas (en particulier si vous utilisez des struct, des tableaux, des pointeurs...). Ne définissez que comment il faudrait structurer les différentes données (ce qui correspond aux déclarations), pas comment on s'y prendra pour les utiliser (ce qui correspond aux instructions du programme). |
|
Dans cette partie, nous recherchons le centre de gravité d'un jouet. Supposons, pour cette partie, avoir choisi un modèle extrêmement simple : on se limite à des parallélépipèdes rectangles, toujours orientés parallèlement aux axes du repère (exemple : un assemblage de briques LEGO ® ). Chaque brique est définie par les coordonnées d'un coin (celui correspondant aux x, y et z minimaux) et ses trois longueurs (en x, y et z). On suppose se limiter à 100 briques au maximum.
Soient les déclarations globales suivantes :
typedef struct brique
{
float x; float y; float z;
float lx; float ly; float lz;
}brique;
#define MAXI 100;
typedef brique tableau[MAXI];
et le programme principal suivant :
void main(void)
{
tableau lego;
int nb;
printf("nombre de briques ?");
scanf("%d",&nb);
saisie(lego,nb);
recherche_CdG(lego,nb);
}
Question 2-1 : écrire en C la fonction saisie, qui demande à l'utilisateur les positions (x,y,z) et dimensions dans les 3 axes (lx,ly,lz) de chacune des briques.
Question 2-2 : Que faut-il modifier dans main et dans saisie pour que la saisie de nb puisse se faire dans saisie plutôt que dans main (sans ajouter de variables globales) ?
Question 2-3 : Ecrire en C une fonction appelée volume qui reçoit en entrée une brique du tableau lego et retourne un flottant valant le volume de cette brique. Cette fonction doit pouvoir être appelée par exemple par l'instruction :
x=volume(lego[5]);
Ecrire également une fonction appelée volume_total, qui reçoit en argument l'adresse du tableau et le nombre de briques, et qui retourne le volume total (ce qui pourra servir pour évaluer la masse de l'ensemble).
Question 2-4 : Le centre de gravité de chaque brique est supposé se trouver au centre de la brique (donc comme si elle était pleine et composée d'un matériau homogène). Le centre de gravité de l'ensemble est situé en (Xg,Yg,Zg). On calcule Xg en faisant la moyenne des coordonnées X de chaque centre de gravité de chaque brique, pondéré par le volume de la brique (idem pour Yg et Zg). Ecrivez en C la fonction recherche_CdG qui calcule puis affiche à l'écran les coordonnées du centre de gravité de l'ensemble.
Dans cette partie, nous allons mettre en place quelques outils pour déterminer la surface de sustentation d'une figurine. Supposons que l'on ait déja déterminé l'ensemble des points de contact entre la figurine et son support (supposé plan). Leur nombre est spécifié dans une variable globale entière nb_pts. Ces points sont définis par leurs deux coordonnées x et y, dans deux tableaux (le point n° I a pour coordonnées x[I],y[I], I Î[0,nb_pts[ ). En voici les déclarations :
#define MAX_PTS 100 int nb_pts; float x[MAX_PTS],y[MAX_PTS];
Nous allons rechercher la courbe enveloppe de ces points. C'est un polygone convexe, que l'on définira par ses sommets.
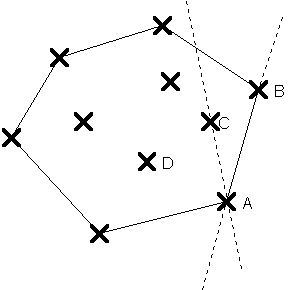 |
Il existe un plusieurs méthodes pour déterminer le polygone convexe englobant tous les points. Je vous propose d'utiliser la suivante : on analyse tous les couples de points possibles. Pour chacun de ces couples, on détermine la droite passant par ces deux points, et l'on teste la position de tous les autres points. S'ils sont tous du même côté, et uniquement dans ce cas, le couple forme un segment de la frontière. Par exemple, le segment AB fait partie de l'enveloppe car tous les autres points sont du même côté de la droite AB, mais le segment AC n'en fait pas partie car B et D sont de part et d'autre de la droite AC. |
Bien que vous sachiez tous comment vérifier de quel côté d'une droite est un point, je vais vous en rappeler une méthode : tous les points (de coordonnées X,Y) situés du même côté d'une droite AB (coordonnées du point A : XA,YA, de B : XB,YB) génèrent tous une valeur VAL= (XA-X)(YB-YA) - (YA-Y)(XB-XA) du même signe. (On pourrait le démontrer par un simple produit vectoriel).
Question 3-1 : Ecrire en C une fonction appelée signe_cote qui :
Question 3-2 : Ecrire en C une fonction appelée est_frontiere qui reçoit en argument d'entrée deux entiers : les indices, dans les tableaux x et y, de deux points (A et B) définissant un segment; et retourne un entier valant 1 si tous les autres points sont du même côté du segment AB (donc ont une valeur VAL de même signe), et valant 0 dans le cas contraire.
Rappel : deux réels sont de même signe si leur produit est positif.
Question 3-3 : Ecrire en C une fonction appelée bonus_un_pt qui ne reçoit aucun argument en entrée, qui ne retourne rien, dont l'action consiste simplement à écrire à l'écran le texte "j'ai lu le sujet jusqu'au bout" puis passe le curseur en début de ligne suivante.
pour voir une correction, cliquez ici
pour retourner au sommaire des sujets d'examen, cliquez ici
Patrick TRAU, ULP - IPST février 2000