
1) Analysons tous les cas possibles, dans un tableau de Karnaugh.

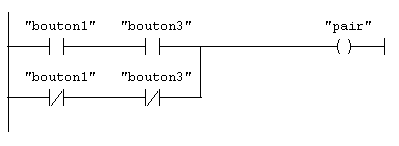
le programme CONT correspondant n'utilise pas b2 (ajouter 2 ne change pas la parité) bien que je l'ai prévu dans les mnémoniques (et d'ailleurs quand j'appuie sur b2 ça ne change pas la sortie).
2) notons D le fait qu'il y ait plus de pièces à droite qu'à gauche, G plus à gauche, E égalité (la position des pièces (en 1 ou 2) ne sera pas prise en compte, uniquement leur nombre (0, 1 ou 2). Cherchons leurs équations. Ces trois états sont exclusifs (si l'un vaut 1 les deux autres valent 0), pour économiser du papier je ne fais qu'un tableau de Karnaugh au lieu de trois :
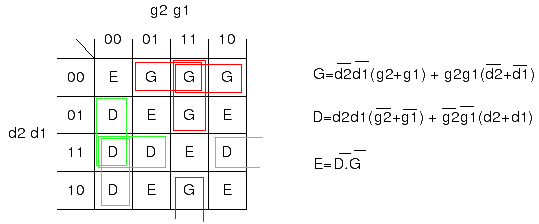
On pourrait aussi calculer E en fonction des entrées, mais l'équation sera bien longue, autant réutiliser ce qu'on a déjà fait. Il ne reste plus qu'à dire qu'on va à droite (AD) si on en a plus à gauche (G) ou que l'on a égalité mais que l'aiguillage est positionné à gauche au moment ou pp détecte la pièce. Idem pour la droite : AD=pp.(G+E.g) AG=pp.(D+E.d)
réseau 1 : quand-est-ce qu'il y en a plus à gauche ?
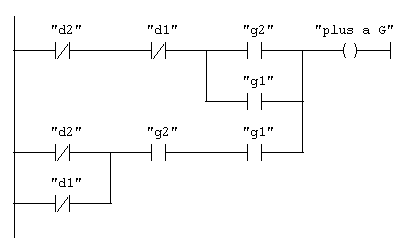
réseau 2 : quand-est-ce qu'il y en a plus à droite ?
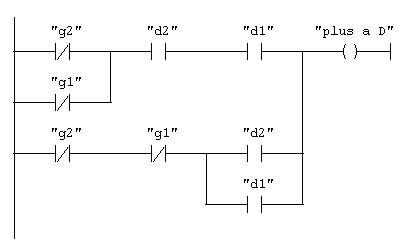
réseau 3 : quand-est-ce qu'il y en autant des deux côtés ?

Réseau 4 : quand aller réellement à droite ?
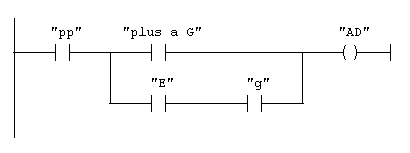
Réseau 5 : quand aller réellement à gauche ?

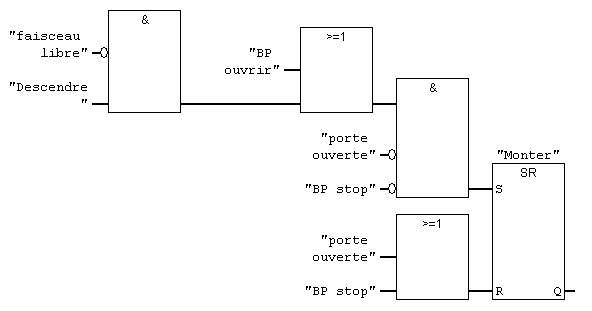
3) On se pose en fait 4 questions (2 par sortie) : quand-est-ce que on doit allumer la montée, quand est-ce qu'on doit l'éteindre, idem pour la descente. Ces 4 cas sont combinatoires (ils dépendent uniquement de l'état des capteurs). Il faut prévoir ce qui se passe dans tous les cas, par exemple si on appuie en même temps sur le bouton montée et celui de descente. Par exemple on monte quand on demande montée (indépendamment de la descente), mais on ne descend que si on a demandé la descente et pas la montée. Si on demande la montée alors qu'on est en train de descendre, il faut allumer la montée mais aussi penser à éteindre la descente.
Réseau 1 : Montée
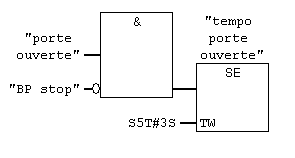
Réseau 2 : temporisation "porte ouverte"
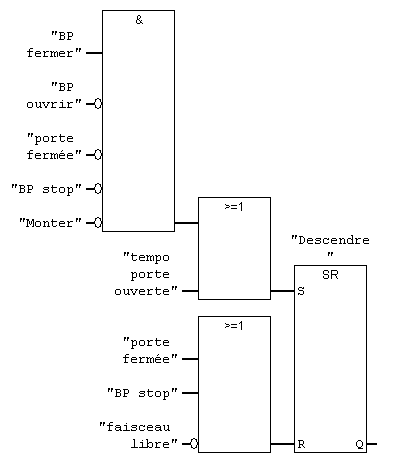
Réseau 3 : descente
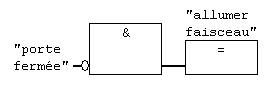
Réseau 4 : faisceau
Patrick TRAU - IPST - ULP - Dec 2006