Licence Technologie Mécanique
Examen d’informatique
Première session 2005

Durée : 2h. Notes de cours personnelles (manuscrites ou polys et sorties imprimante), TD et TP autorisés. Calculatrices autorisées. Autres documents (dont livres) interdits. Calculatrices autorisées. Ce sujet comporte 3 pages (et 6 questions).

Nous désirons créer un programme d'analyse de treillis (dans le plan). Un treillis est un assemblage de barres (généralement des profilés rectilignes), assemblées entre elles en des endroits appelés "noeuds". Pour ce sujet, nous allons admettre les hypothèses suivantes :

• systèmes plans (géométrie, chargement et déplacements tous dans le même plan).
• Les barres sont articulées aux noeuds (liaison rotule). En fait, même si c'est rarement le cas (liaison complète soudée, rivée, boulonnée...), les liaisons ne peuvent effectivement pas transmettre un couple du fait du manque de raideur des barres.
• Les charges extérieures sont uniquement appliquées aux noeuds (si un autre chargement est appliqué à une barre, un calcul de statique simple permet d'en trouver l'équivalent, uniquement appliqué aux extrémités, ceci bien sûr après avoir vérifié la résistance de la barre à cette sollicitation).
• Des deux hypothèses précédentes découle le fait que les barres, soumises uniquement à deux forces, ne travaillent qu'en traction/compression. Nous supposerons que les barres en compression ont un profil empêchant le flambage.
• Nous négligerons le poids des barres (et ne pourrons donc pas étudier la tour Eiffel).
• Le système est triangulé et isostatique (soient nbn le nombre de noeuds et nbb le nombre de barres, alors 2*nbn - nbb = 3 )

Si d'autres hypothèses vous semblent nécessaires, faites les (mais justifiez les aussi).

Exemple de treillis : voir figure 2 (en fin du sujet).

Question 1 : Pour représenter en mémoire la géométrie d'un treillis, nous allons utiliser une zone commune. Nous aurons au maximum 100 noeuds (et donc 2*100-3=197 barres). Le nombre de noeuds réels est nommé nbn. Pour chaque noeud, on stocke ses coordonnées réelles, dans deux tableaux nommés X et Y. Chaque noeud est identifié par son numéro entre 1 et nbn (contrairement à la figure où il est identifié par une lettre), ce numéro correspondra à la position, dans les tableaux X et Y, de ses coordonnées. Les barres (on nomme nbb leur nombre) sont définies par deux tableaux, nommés N1 et N2, contenant, pour chaque barre, le numéro du premier et second noeud de la barre.

• 1A) Déclarez ces données (en zone commune)
• 1B) Ecrivez un sous-programme permettant la saisie de ces données (nbn, puis les coordonnées des noeuds, puis les barres), un autre pour l'affichage (ils pourront accéder directement à la zone commune)

Question 2 : Ecrivez une fonction recevant en argument un numéro de noeud, qui détermine (et retourne, mais ne l'affiche pas) le nombre de barres attachées à ce noeud. Cette fonction sera utile lors de la recherche de la somme des forces en un noeud.

Question 3 : Ecrivez une fonction recevant en argument un numéro de barre, et retournant la longueur de celle-ci :

Question 4 : Ecrivez une fonction qui affiche le numéro de la barre la plus longue. En cas d'égalité, elle en affiche une (n'importe laquelle dans toutes celles qui ont la longueur maximale), mais prévient qu'il y en a plusieurs et en affiche le nombre

Question 5 : Ecrivez une fonction qui reçoive en argument un numéro de barre B , et un numéro de noeud N (celui-ci sera obligatoirement un des deux noeuds de la barre, inutile de le vérifier). Cette fonction retournera un réel positif si l'autre noeud de la barre B est plus à gauche que N, 0 s'ils ont le même X, et négatif s'il est plus à droite. La valeur absolue de ce réel retourné sera DX/L (correspond au cosinus de l'angle entre la barre et l'horizontale, côté adjacent sur hypoténuse). Cette question rapporte peu de points.

Question 6 : Pour résoudre le système, une méthode est d'écrire toutes les équations d'équilibre aux noeuds (somme des forces = 0), ainsi qu'aux barres (deux forces, donc égales et opposées), et à l'ensemble (force et moment), puis résoudre le système. Nous n'allons pas résoudre le système ici, mais nous (vous, plutôt) allons préparer le calcul, en particulier l'équilibre aux noeuds. En un noeud nous avons en fait deux équations : une en X et une en Y. Les forces appliquées à ce noeud sont le chargement extérieur (que nous mettons dans le second membre, non traité dans cette question), et les efforts des barres, tous colinéaires aux barres. Nous allons créer un "premier membre" qui est une matrice de 2*nbn lignes (deux par noeud, une en X et une en Y), et nbb colonnes (une par barre). La première ligne de cette matrice représente l'équation en X de l'équilibre du premier noeud. Elle comportera donc une valeur entre -1 et 1 pour chacune des barres connectées à ce noeud (représentant la proportion de l'intensité de la force projetée sur X, donc le cosinus de l'angle, positif pour les barres à gauche du noeud, négatif sinon, et calculé dans la question 5), 0 pour toutes les autres barres. La seconde ligne traite du même noeud, en Y. Les lignes suivantes traitent les autres noeuds, de la même manière.

• 6a) déclarez cette matrice, par exemple dans une seconde zone commune mais ce n'est pas obligatoire).
• 6b) écrivez un sous-programme nommée equilibreX qui reçoit en argument un numéro de noeud et une ligne, qui remplisse cette ligne d'après l'explication ci-dessus, et la figure ci-dessous. Les données décrites à la question 1 sont bien évidement supposées connues ici, ainsi que les fonctions et sous- programmes des questions précédentes, même si vous ne les avez pas tous terminés.
• 6c) en supposant que le sous-programme equilibreY ait également été écrit, écrivez le sous-programme defmatrice qui crée la matrice complète.

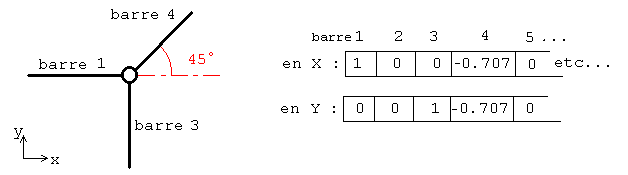
figure 1 : exemple d'équilibre en un noeud

Question 7 (cours) : Le serveur web de l'IPST a pour url «http://www-ipst.u-strasbg.fr», alors que celui de l'iut de Tours est «http://www.iut.univ-tours.fr». Que révèle cette petite différence de points et tirets ?

Remarques : les questions sont indépendantes. Essayez de répondre au maximum de questions, même sans fignoler les détails. Pensez à expliquer (un peu) ce que vous faites. Si vous ne comprenez pas mon organisation des données, vous pouvez à la rigueur m'en proposer une autre.

Schéma fig 2:

schéma tiré du livre "mécanique 1ères F, tome 1" de Lemasson et Gal (édité chez Dunod).

Caractéristiques géométriques :

Description des noeuds Description des barres