

Licence
Technologie Mécanique
Examen d’informatique
Première
session 2004
Durée : 2h. Notes de cours personnelles (manuscrites ou polys et sorties
imprimante), TD et TP autorisés. Calculatrices autorisées.
Autres documents (dont livres) interdits. Calculatrices autorisées.
Le calcul
d'une pièce par éléments finis consiste à
découper la pièce en petits éléments, en
supposant un comportement simplifié (par exemple linéaire)
pour chaque élément, permettant d'appréhender le
comportement global de la pièce. Comme pour l'approximation
d'une courbe par des segments de droites, la taille des éléments
n'a pas nécessairement à être uniforme.
 Plaçons
nous uniquement dans les cas bidimensionnels. Un maillage d'une pièce
est le découpage en éléments simples. Nous nous
limiterons aux éléments triangles comme dessiné
ci-contre. Le maillage est défini par deux groupes de
données : les noeuds (numérotés ici de 1 à
9) et les élément (numérotés ici de I à
VIII). Chaque noeud est défini par ses coordonnées X et
Y, chaque élément par les numéros des trois
noeuds qui le forment.
Plaçons
nous uniquement dans les cas bidimensionnels. Un maillage d'une pièce
est le découpage en éléments simples. Nous nous
limiterons aux éléments triangles comme dessiné
ci-contre. Le maillage est défini par deux groupes de
données : les noeuds (numérotés ici de 1 à
9) et les élément (numérotés ici de I à
VIII). Chaque noeud est défini par ses coordonnées X et
Y, chaque élément par les numéros des trois
noeuds qui le forment.
Question
1) Ecrivez un sous-programme de saisie des noeuds : il demande le
nombre de noeuds, puis, pour chaque noeud, ses coordonnées.
Les coordonnées seront stockées dans deux tableaux de
réels, transmis en arguments. Le nombre de noeuds sera
également un argument du sous-programme. Ecrivez un autre
sous-programme pour la saisie des éléments. Il demande
le nombre d'éléments, puis pour chaque élément
les numéros des trois noeuds qui le composent. Les numéros
de noeuds seront stockés dans trois tableaux d'entiers,
transmis en arguments. Le nombre d'éléments sera
également un argument du sous-programme. Vu la longueur du
sujet, ne perdez pas de temps en tests superflus (ceci vaut aussi
pour les questions suivantes).
Exemple
très simple pour comprendre comment seront stockées les
données :
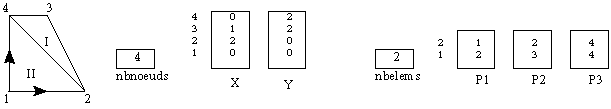
Question
2) Ces données pourraient être connues partout grâce
à un common. Ecrivez ce common et un programme de test qui
déclare ces données et appelle les deux sous-programmes
de la question 1 (sans les changer). Les noms des variables
communes devront être celles de l'exemple simple précédent.
Supposons par exemple nous limiter à 10000 noeuds et 10000
éléments maximum. Vous pourrez réutiliser ce
common dans les questions qui suivent.
Question
3) Les calculs sont plus simples si l'on est sûr que les
trois noeuds définissant chaque élément sont
donnés dans le sens trigonométrique. C'est à
dire que, si on les nomme P1, P2, P3, alors la composante sur Z du
produit vectoriel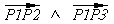 doit
être positif. Ecrivez pour commencer une fonction à qui
l'on donne en argument trois numéros de points (en plus
d'autres arguments ou common si nécessaire) et qui retourne un
logical qui vaille .true. si les trois points sont donnés dans
le sens trigonométrique (et .false. sinon). Puis écrivez
un sous programme qui réorganise tous les éléments
pour qu'ils soient tous définis en sens trigonométrique
(en échangeant les points 2 et 3 si nécessaire).
doit
être positif. Ecrivez pour commencer une fonction à qui
l'on donne en argument trois numéros de points (en plus
d'autres arguments ou common si nécessaire) et qui retourne un
logical qui vaille .true. si les trois points sont donnés dans
le sens trigonométrique (et .false. sinon). Puis écrivez
un sous programme qui réorganise tous les éléments
pour qu'ils soient tous définis en sens trigonométrique
(en échangeant les points 2 et 3 si nécessaire).
Question
4) La résolution par éléments finis
nécessite d'analyser l'équilibre de chaque noeud sous
l'action des différents éléments qui s'y
raccordent. Il est donc utile de disposer d'un fonction à qui
l'on donne en argument un numéro de point, et qui retourne le
nombre d'éléments qui possèdent ce point.
Ecrivez cette fonction.
Question
5) La résolution par éléments finis est
également fortement influencée par l'ordre de
numérotation des noeuds. Nous n'allons pas tout renuméroter,
mais écrivez déjà un sous-programme qui permette
d'échanger deux noeuds dont on donne (en argument) leur
numéros. Ceci consiste dans un premier temps à échanger
les coordonnées des deux noeuds dans les deux tableaux des
coordonnées, puis de changer le numéro de noeud dans
tous les éléments contenant l'un ou les deux noeuds.
Question
6) On appelle arête les côtés des éléments
(donc dans notre cas, il y a trois arêtes par élément).
Une arrête est définie par ses deux noeuds. Il est
particulièrement important de savoir si une arête fait
partie de la frontière ou de l'intérieur de la pièce.
Une arrête est interne si elle appartient à deux
éléments. Elle est frontière si elle
n'appartient qu'à un seul élément. Ce n'est pas
une arête si le couple de noeuds n'apparaît dans aucun
élément. Si les données sont correctement
entrées, une arrête ne peut pas appartenir à plus
de deux éléments. Ecrivez une fonction qui, pour un
couple de noeuds, donne le nombre d'éléments qui
contiennent cette arrête. Puis écrivez une fonction qui
affiche l'ensemble des arrêtes frontière d'un maillage.
Remarques
: Si le sujet n'est pas assez précis dans certains cas,
faites l'hypothèse que vous préférez, mais
n'oubliez pas d'expliciter vos suppositions sur la copie. Si vous
n'arrivez pas à retrouver la syntaxe exacte d'une
fonctionnalité du Fortran, expliquez en français ce que
vous voulez faire. Si vous avez du mal avec les arguments et
sous-programmes, il vaut mieux juste mettre les instructions qui
feraient partie d'un gros programme principal que rien.
pour retourner au sommaire des sujets d'examen, cliquez ici
Si vous le désirez, vous pouvez regarder ici une proposition de réponses.
Patrick TRAU, ULP - IPST fev 04
 Plaçons
nous uniquement dans les cas bidimensionnels. Un maillage d'une pièce
est le découpage en éléments simples. Nous nous
limiterons aux éléments triangles comme dessiné
ci-contre. Le maillage est défini par deux groupes de
données : les noeuds (numérotés ici de 1 à
9) et les élément (numérotés ici de I à
VIII). Chaque noeud est défini par ses coordonnées X et
Y, chaque élément par les numéros des trois
noeuds qui le forment.
Plaçons
nous uniquement dans les cas bidimensionnels. Un maillage d'une pièce
est le découpage en éléments simples. Nous nous
limiterons aux éléments triangles comme dessiné
ci-contre. Le maillage est défini par deux groupes de
données : les noeuds (numérotés ici de 1 à
9) et les élément (numérotés ici de I à
VIII). Chaque noeud est défini par ses coordonnées X et
Y, chaque élément par les numéros des trois
noeuds qui le forment.
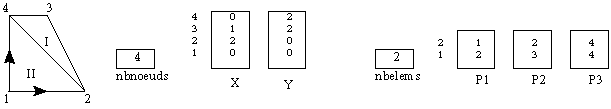
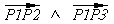 doit
être positif. Ecrivez pour commencer une fonction à qui
l'on donne en argument trois numéros de points (en plus
d'autres arguments ou common si nécessaire) et qui retourne un
logical qui vaille .true. si les trois points sont donnés dans
le sens trigonométrique (et .false. sinon). Puis écrivez
un sous programme qui réorganise tous les éléments
pour qu'ils soient tous définis en sens trigonométrique
(en échangeant les points 2 et 3 si nécessaire).
doit
être positif. Ecrivez pour commencer une fonction à qui
l'on donne en argument trois numéros de points (en plus
d'autres arguments ou common si nécessaire) et qui retourne un
logical qui vaille .true. si les trois points sont donnés dans
le sens trigonométrique (et .false. sinon). Puis écrivez
un sous programme qui réorganise tous les éléments
pour qu'ils soient tous définis en sens trigonométrique
(en échangeant les points 2 et 3 si nécessaire).