

on regroupe les données d'une tâche dans un structure : son nom, sa durée (pour permettre un intervalle un intervalle de tolérance, on peut donner deux durées : mini - maxi). Pour les ressources humaines, un entier suffit à définir le nombre de personnes nécessaires.
Pour les antériorités, il faut prévoir des pointeurs vers les tâche suivantes. Le problème est leur nombre. Si il y en a toujours peu, on peut créer un tableau statique (par exemple si jamais plus de 3), sinon il faudra utiliser un tableau dynamique (créé par un malloc).
Pour les ressources matérielles, il faudrait soit simplement prévoir un nombre suffisant de caractères, mais si on désire gérer ces ressources par le programme il faudrait un tableau annexe définissant toutes les ressources existantes, chaque ressource sera donc identifiée par un entier (sa position dans le tableau) ou un pointeur. Dans un tâche, il suffirait d'inclure la liste de ces entiers (sous forme d'un tableau statique si leur nombre est toujours restreint, dynamique sinon). Vu l'exemple donné dans le sujet, il était inutile de trop parler des ressources matérielles
#define LONGUEUR_NOM 10
#define MAXI_TACHES 1000
typedef struct tache
{
char nom[LONGUEUR_NOM]; //si on avait du temps, on prendrait un tableau dynamique
int nb_ress; //nombre de ressources (humaines uniqument) nécessaires
float min,max; //limites de durée
int nb_suiv;
struct tache **suiv; //ou *suiv[] : tableau (dynamique) d'adresses de tâches
}tache;
typedef tache tableau[MAXI_TACHES];
A priori, pour représenter un arbre, il vaut mieux utiliser des pointeurs. A un niveau donné, une tâche de base gardera des antériorités par rapport aux autres tâches de même niveau, donc comme à la question précédente. Mais (si elle peut se décomposer) elle pointera vers un autres réseau de tâches : celles qui la composent. Si les sous-tâches commencent toujours par une tâche unique, il suffit d'un seul pointeur, ce n'est pas trop compliqué. S'il peut y en avoir plusieurs, le plus simple est de créer une tache unique, de durée 0, qui pointera vers les autres.
#define DIM 20
typedef int tableau[DIM};
void main(void)
{
int i,N;
tableau A1,A2;
printf("combien de tâches ?");
scanf("%d",&N);
for(i=0;i<N;i++)
do //évidement la vérification des réponses n'était pas obligatoire
{
printf("antérorités de la tâche %d (-1 si rien) ?");
scanf("%d %d", A1+i,A2+i);
}while(A1[i]<-1||A2[i]<-1|| A1[i]>=N|| A2[i]>=N);
/* on aurait aussi pu demander le nombre d'antériorités, puis demander les valeurs
sans que l'utilisateur n'ait à entrer les -1 */
}
void affiche(tableau t, int nb)
{
int i;
printf(" [ ");
for(i=0;i<nb;i++)printf("%d ",t[i]);
printf("] \n");
}
on rajoutera à la fin de main :affiche(A1,N); affiche(A2,N);
int incoherence(int N, tableau A1, tableau A2)
{
tableau valide;
int i,nb=0,modif;
//mettons 1 (vrai) dans "valide" pour ceux qui n'ont aucune antériorité, 0 pour les autres
for(i=0;i<N;i++)valide[i]=((A1[i]==-1)&&(A2[i]==-1));
do //validons ceux dont les antériorités sont valides
{
modif=0;
for(i=0;i<N;i++)
if(!valide[i] && (valide[A1[i]]||(A1[i]==-1)) && (valide[A2[i]]||(A2[i]==-1)))
valide[i]=modif=1;
} while(modif); //et recommençons jusqu'à ce qu'on n'en trouve plus
for(i=0;i<N;i++)if(!valide[i])nb++; //il ne reste plus qu'à les compter
return(nb);
}
void classer(int N, tableau A1, tableau A2, tableau classement)
// le 3ème argument sera celui dans lequel il y aura la liste triée
{
int i,c=0;
tableau deja_pris; //ce tableau sera effacé à la sortie de la fonction
//cherchons déjà ceux n'ayant aucune antériorité
for(i=0;i<N;i++)
if(A1[i]==-1 && A2[i]==-1)
{classement[c++]=i;deja_pris[i]=1;}
else
deja_pris[i]=0;
do //recherchons ceux (pas encore pris) dont les antériorités sont déjà prises
{
for(i=0;i<N;i++)
if(!deja_pris[i] && (deja_pris [A1[i]]||(A1[i]==-1)) && (deja_pris [A2[i]]||(A2[i]==-1)))
{classement[c++]=i;deja_pris[i]=1;}
} while(c<N); //et recommençons tant qu'on ne les a pas tous pris
#define MAX 100
typedef struct tache
{
float duree;
char r1;
char r2;
}tache;
typedef tache tab[MAX];
tab t;
int N;
float duree_tot(tab t, int n)
{
int i;
float tot;
tot=t[0].duree; //on ne peut pas le faire en même temps que le précédent, c'est le premier
for(i=1;i<n;i++)
if(t[i].r1==t[i-1].r1 || t[i].r1==t[i-1].r2 || (t[i].r2 && (t[i].r2==t[i-1].r1 || t[i].r2==t[i-1].r2)))
tot+=t[i].duree; //s'il y a ressource commune, on le fait séparément du précédent
else if (t[i].duree>t[i-1].duree)tot+=(t[i].duree-t[i-1].duree); //on peut chevaucher, mais il n'y a pas assez de temps disponible
/* sinon (cette tâche est plus courte que la précédente et pas de ressource
commune) on les fait en même temps, il n'y a rien à ajouter à la durée totale ! */
return(tot);
void echange (tab t, int i) //je suppose qu'on a donné i<N-1, bien sûr
{
tache tampon;
memcpy(&tampon, t+i+1); //on pouvait également copier les 3 champs
memcpy(t+i+1,t+i);
memcpy(t+i,&tampon);
}
Vu le nombre assez limité de tâches, on peut essayer toutes les combinaisons. On calcule la durée actuelle. Puis on échange les deux premiers, on calcule la durée et si c'est mieux on valide l'échange, sinon on les remet comme initialement. Puis on essaye en échangeant le second et le troisième, et ainsi de suite.
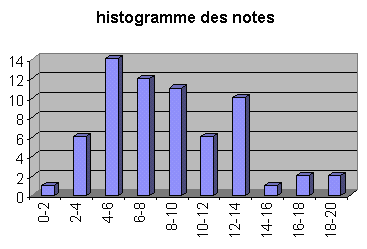
Remarque : Ceci n'est qu'une proposition. Des réponses différentes pouvaient être bonnes, ou partiellement bonnes (ou aussi pas trop bonnes voire carrément nulles). Puisque vous êtes si curieux(se), voici les notes obtenues, et l'histogramme :


Patrick TRAU, ULP - IPST juin 2001