
Université Louis Pasteur Juillet 2000
Durée : 2h. Cours manuscrits, correction des TP, documents distribués en cours et photocopies des documents publiés sur le web par Mr Trau autorisés.
Vu les résultats de la coupe de robotique E=M6 2000, vous avez décidé de participer, vous aussi, à la prochaine édition. En attendant de connaître le nouveau règlement, vous vous proposez d'ajouter de nouvelles fonctionnalités au champion de France 2000 :
Les questions ci dessous ne tenteront pas de résoudre la globalité du problème, mais chaque partie traitera un point particulier, avec des hypothèses simplificatrices qui ne sont pas les mêmes pour les deux parties, qui sont donc indépendantes et peuvent être traitées dans l'ordre qui vous convient (et même les questions, à condition de bien les numéroter).
Le déplacement du robot est obtenu par la rotation de deux roues, commandée chacune indépendamment par un moteur pas à pas. Si les deux moteurs sont réglés à la même vitesse, le robot va tout droit. Sinon il tourne du côté du moteur le plus lent.
Le robot est initialement placé dans une position A et une direction connue. On désire amener le chariot dans une position B, dans une direction donnée. Les deux directions sont définies, en plus de A et B, par leur point d'intersection C. Afin de minimiser les variations de rotation du chariot (les rotations sont saccadées et génèrent, du fait qu'ils restent parallèles, un glissement important des pneus, cf. le char d'assaut qui utilise également ce principe) on désire utiliser une trajectoire parabolique (tangente à la direction de départ et celle d'arrivée). Ceci minimisera les variations de vitesse du CIR (centre instantané de rotation).

Nous utiliserons une représentation paramétrique de la parabole : un paramètre u variant de 0 à 1 nous permet de décrire la parabole de A (pour u=0) vers B (pour u=1). Vous n'allez pas ici déterminer l'équation de la parabole (bien que vous devriez en être capables), supposons que vous l'ayez fait, et que vous ayez déjà écrit deux fonctions (elles sont dans le fichier "parabole.h") dont les entêtes sont : float calculeX(float u) et float calculeY(float u) qui pour un u donné retournent respectivement les deux coordonnées du point correspondant de la parabole. Ces deux fonctions utilisent les variables globales float XA,YA,XB,YB,XC,YC; qui devront avoir été définies auparavant.
Question 1.1 : faites un programme répondant au cahier des charges suivant : il demande les coordonnées des points A,B,C, et le nombre N de pas intermédiaires désirés. Pour u variant de 0 à 1 par pas de 1/N, à chaque pas affichez à l'écran de combien on doit se déplacer en X et en Y (donc par rapport au point précédent). Donnez toutes les instructions et directives nécessaires pour faire fonctionner ce programme, seul le fichier "parabole.h" n'a pas à être écrit. Votre programme devra également vérifier que les données fournies par l'utilisateur sont plausibles.
Question 1.2 : évidement, les mouvements en X et Y dans un repère fixe ne sont pas d'une grande utilité pour notre robot, il faudrait plutôt les déterminer dans un repère local R, lié au robot, qui pourrait être défini, par rapport à un repère fixe R0 , par un déplacement (position XG , YG du centre de gravité du robot par exemple) et une direction (angle A par rapport à X0 par exemple). Ecrivez une fonction de changement de base : on lui fournit en arguments X et Y, position d'un point dans R0, ainsi que la position de R (XG , YG et A), la fonction doit modifier X et Y pour qu'ils représentent en fin de fonction la position du même point mais dans R0. (indice : je veux des passages d'arguments par adresse et d'autres par valeur). La fonction n'a pas à afficher quoi que ce soit à l'écran (d'ailleurs il n'y a pas d'écran sur le robot).
Vu le prix particulièrement attractif des mini-caméras vidéo (de qualité certes assez médiocre), nous allons essayer de donner la vue à notre robot. Supposons disposer d'une telle caméra, et de sous programmes permettant de l'utiliser (tous définis dans le fichier "camera.h"). Dans un premier temps, pour éviter des traitements trop compliqués, nous avons réglé notre caméra en mode noir et blanc (256 niveaux de gris : 0 correspond à un pixel noir, 255 un blanc), en définition 640x480. Je vous rapelle qu'en C, les "unsigned char" peuvent s'utiliser comme des entier, mais sont limités à la plage [0,256[.
Dans "camera.h", il y a entre autres :
typedef unsigned char pixel; #define LARG 640 #define HAUT 480 typedef pixel ligne[LARG]; typedef ligne image[HAUT]; void capture_image(image t); /* met dans t l'image fournie par la caméra */
Nous voulons déterminer la taille d'un obstacle situé devant le robot (on le suppose sombre, le fond étant clair, la limite sera stockée dans une variable appelée "seuil").
Question 2.1 : en partant du milieu de l'écran écrivez une fonction qui va horizontalement vers la droite, jusqu'à trouver la limite de l'obstacle (pixel>seuil), puis fait de même vers la gauche, et retourne la largeur apparente de l'obstacle.
Question 2.2 : Cette largeur n'est pas suffisante, nous allons chercher à déterminer plus précisément la taille et même la forme de l'obstacle. Supposons que l'on ait déja déterminé un ensemble des points appartenant à l'obstacle.. Leur nombre est spécifié dans une variable globale entière nb_pts. Ces points sont définis par leurs deux coordonnées x et y, dans deux tableaux (le point n° I a pour coordonnées x[I],y[I], I Î [0,nb_pts[ ). En voici les déclarations :
#define MAX_PTS 100 int nb_pts; float x[MAX_PTS],y[MAX_PTS];
Nous allons rechercher la courbe enveloppe de ces points. C'est un polygone convexe, que l'on définira par ses sommets.
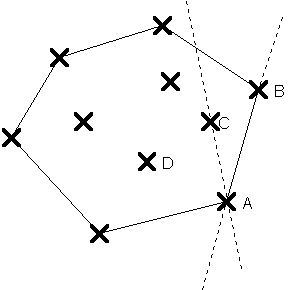 |
Il existe plusieurs méthodes pour déterminer le polygone convexe englobant tous les points. Je vous propose d'utiliser la suivante : on analyse tous les couples de points possibles. Pour chacun de ces couples, on détermine la droite passant par ces deux points, et l'on teste la position de tous les autres points. S'ils sont tous du même côté, et uniquement dans ce cas, le couple forme un segment de la frontière. Par exemple, le segment AB fait partie de l'enveloppe car tous les autres points sont du même côté de la droite AB, mais le segment AC n'en fait pas partie car B et D sont de part et d'autre de la droite AC. |
Bien que vous sachiez tous comment vérifier de quel côté d'une droite est un point, je vais vous en rappeler une méthode : tous les points (de coordonnées X,Y) situés du même côté d'une droite AB (coordonnées du point A : XA,YA, de B : XB,YB) génèrent tous une valeur VAL= (XA-X)(YB-YA) - (YA-Y)(XB-XA) du même signe. (On pourrait le démontrer par un simple produit vectoriel). Ecrivez en C une fonction appelée signe_cote qui :
N'écrivez pas une fonction appelée est_frontiere qui recevrait en argument d'entrée deux entiers : les indices, dans les tableaux x et y, de deux points (A et B) définissant un segment ; et retourne un entier valant 1 si tous les autres points sont du même côté du segment AB (donc ont une valeur VAL de même signe), et valant 0 dans le cas contraire.
Remarque : répondre uniquement à la question 2.2, surtout en ayant pensé à apporter les bons documents, n'apportera pas énormément de points
pour retourner au sommaire des sujets d'examen, cliquez ici
Patrick TRAU, ULP - IPST septembre 2000