Durée : 1h30. Cours et documents distribués en cours autorisés
1) Simplifiez l'équation suivante, et tracez le circuit correspondant, à l'aide de portes combinatoires
2) calculez 
et simplifiez au maximum le résultat, sachant que :
Rappel : 
représente l'opérateur ou exclusif.
3) Effectuez la division entière suivante (en binaire), en posant les calculs intermédiaires, puis traduisez votre résultat en décimal pour vérifier vos calculs :
4) Un tapis roulant transporte des pièces de quatre types différents, numérotés 0,1,2 et 3. Ces pièces sont solidaires d'un support comportant une plaque rectangulaire, percée d'un ou deux trous permettant de définir le type de pièce :
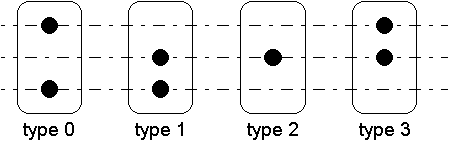
Trois capteurs optiques (notés i, j et k), alignés verticalement, permettent de lire le type inscrit sur une plaque passant devant eux, donnant 1 si le rayon n'est pas coupé (donc en face d'un trou ou pas de plaque) et 0 dans le cas contraire.
On désire créer un composant (à l'aide de portes logiques) qui à partir de trois entrées (reliées à i, j et k) génère 4 sorties :
Remarque : les capteurs ne pouvant pas être parfaitement alignés, on considère que quand on obtient sur i,j,k des valeurs imprévues, c'est qu'il y a bien une plaque présente, mais qui n'est pas exactement en face des capteurs.
Trouvez les équations définissant ce composant et faites en le schéma (à l'aide de portes combinatoires)
5) A l'aide de portes et de bascules supplémentaires, modifiez le composant de la question 4 pour qu'il donne sur T0 et T1 :
Remarque : vous pouvez traiter les questions dans le désordre (mais numérotez-les).