
convexe
non convexe (mais l'algorithme cité plus bas fonctionnerait)
vraiment pas convexe
Durée : deux heures. Documents autorisés : notes prises en cours et documents distribués par l'enseignant.
Un fabricant de circuits imprimés cherche à optimiser sa production. Il lui faut analyser chaque type de cartes produites, et en particulier le ratio surface conductrice/surface totale de la carte. Pour une carte, on dispose bien entendu de l'information de sa surface totale (en général la carte est rectangulaire mais pas toujours, dans le cas de cartes à insérer dans encombrement limité). On dispose également d'un fichier définissant toutes les pistes. Une piste est une surface (rarement convexe) mais que l'on supposera connexe, avec une frontière en un seul morceau. La piste est définie par sa frontière. On supposera ici que la frontière la piste n'est composée que de segments de droites (en particulier les cercles seront approximés par un polygone régulier).
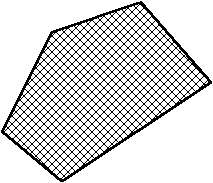
Exemples respectant ces conditions :
|
|
|
convexe |
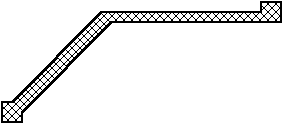
non convexe (mais l'algorithme cité plus bas fonctionnerait) |
vraiment pas convexe |
Exemple ne respectant pas ces conditions :
|
|
refusé : frontière en deux parties, cercle |
accepté (non convexe) |
La frontière est représentée en mémoire sous forme d'une suite ordonnée de sommets (sous forme d'un tableau statique appelé Frontiere, pour simplifier). La frontière est l'ensemble des segments reliant ces sommets (la frontière est fermée, le dernier sommet est relié au premier). Chaque sommet est représenté par une structure comportant deux champs (x et y, les coordonnées du point). La variable NbSommets contient le nombre de sommets (et donc de segments) de la frontière. Ces données sont déclarées globalement au début du fichier programme, grâce aux déclarations ci dessous :
#define MAXSOMMETS 200
typedef struct {float x; float y; } sommet;
typedef sommet tableau[MAXSOMMETS];
tableau Frontiere;
int NbSommets;
Puisque ces déclarations sont globales, elles sont valables pour tout le programme, vous n'avez pas besoin de les recopier dans vos réponses.
La méthode choisie pour calculer l'aire des pistes est d'essayer de décomposer la surface en triangles et trapèzes (dont on sait facilement calculer la surface). On se limitera ici à des triangles et trapèzes à base horizontale. Il suffit de "tracer" des horizontales passant par les sommets pour les trouver :

Nous ne traiterons évidement pas tout le problème aujourd'hui (c'est à dire la fonction main) , vous ne créerez que quelques fonctions. On suppose que Frontiere et NbSommets sont déjà initialisés, par exemple ainsi :

Question 1 : écrivez (en C, bien sûr) la fonction affiche qui affiche à l'écran les coordonnées des différents sommets.
Question 2 : écrivez la fonction perimetre qui retourne la longueur totale de la frontière
Question 3 : écrivez la fonction calculX qui reçoit 5 arguments flottants : X0 et Y0 coordonnées d'un point P0 d'une droite, X1 et Y1 un second point P1 de cette droite (différent de P0), et Y une ordonnée (d'un point P). La fonction doit retourner l'abscisse du point P.
Question 4 : à quoi sert la ligne suivante, à quel endroit du fichier programme a-t-on intérêt à la placer, pourquoi autant de parenthèses ?
#define calculY(X0,Y0,X1,Y1,X) calculX((Y0),(X0),(Y1),(X1),(X))
Question 5 : écrivez la fonction horiz qui reçoit en argument un numéro de segment de la frontière (entre 1 et NbSommets) et l'ordonnée Y d'une droite horizontale, et retourne l'abscisse de l'intersection du segment et de l'horizontale. Le segment numéroté 1 est le segment reliant les sommets 0 à 1 (c'est à dire le premier et le second du tableau), le segment 2 va des sommets 1 à 2, etc... Le segment NbSommets va du dernier sommet au premier.
Question 6 : écrire la fonction surf_trap qui reçoit 6 arguments flottants, dans l'ordre: les abscisses des 2 sommets de la base horizontale d'un trapèze, les abscisses des deux autres sommets, puis les ordonnées des deux bases, et retourne la surface.
Question 7 : Pour décomposer la piste, il va falloir rechercher les différentes horizontales, et les traiter dans un certain ordre. écrivez un bout de programme qui met dans un tableau les ordonnées des différents sommets de la frontière. Si deux sommets ont la même ordonnée, celle-ci n'est pas à répéter dans le tableau. Puis (ou en même temps si vous préférez) triez le tableau par ordre croissant. Je préférerai que le tableau soit dynamique.
remarques générales :
- une fonction qui doit retourner une valeur n'a pas besoin de l'afficher à l'écran.
- dans une question, on peut utiliser le résultat d'une question précédente (même si on ne l'a pas encore traitée), mais pas d'une question suivante.
- la racine carrée est donnée par la fonction sqrt définie en standard dans math.h
- la valeur absolue d'un réel est donnée par la fonction fabs définie en standard dans
math.h
- l'abscisse d'un point est sa coordonnée en X, l'ordonnée en Y.
- la longueur L d'un segment peut se calculer par Pythagore : ![]() (voir cours de maths 3ème)
(voir cours de maths 3ème)
- l'équation d'une droite passant par les points P0 et P1 est (X1-X0)(Y1-Y)=(Y1-Y0)(X1-X) (et non pas Y=aX+b qui ne fonctionne pas avec une verticale, car nécessiterait une division par X1-X0)
- la surface d'un trapèze est la demi somme de ses bases multipliée par la hauteur.