COURBES ET SURFACES

• introduction
• courbes
  • représentation des points
  • polynômes de Lagrange
  • splines
  • courbes de Bezier
    • conditions
    • détermination des polynômes de Bezier
    • forme polynomiale
    • intérêt
    • exemples
• surfaces
  • Coons
  • surfaces de Bezier

introduction

On a souvent besoin de représenter dans l'ordinateur des courbes ou surfaces dont le type n'est soit non classifiable (ni parabole ni cercle...) soit non connu à l'avance. On les regroupe généralement sous le nom de "courbes et surfaces non mathématiques", car l'équation mathématique n'est pas connue par le programmeur. Ces courbes ou surfaces sont en général définies par un ensemble de points, plus ou moins nombreux.

Le problème qui se posait à la Régie Renault consistait à représenter les surfaces de carrosserie dessinées par les designers, pour réaliser les matrices d'emboutissage. La pièce était définie par des sections planes successives. A l'arrivée des machines à commande numérique, la méthode manuelle a dût être abandonnée. Après création d'une maquette 3D (en bois, plâtre,... modifiée au fur et à mesure), la surface était déterminée par une matrice de points obtenus à l'aide d'une machine à mesurer 3D. Pour obtenir une bonne précision, le nombre de points nécessaire est très important. Le nombre de maquettes réalisées en cours de conception étant important (d'où pertes de temps), on a demandé aux stylistes de créer sur ordinateur, les maquettes pouvant alors être facilement et rapidement réalisées en commande numérique. P. Bezier a du mettre au point une méthode permettant de définir la surface par un nombre minimal de points caractéristiques, permettre de modifier facilement la surface par déplacement d'un minimum de points, pouvoir représenter toute surface (y compris plane), sans "cassure" (continûment dérivable).

courbes

représentation des points

Une courbe peut être représentée par :

- son équation explicite (y=f(x) dans le plan, deux équations dans l'espace par exemple y=f(x) z=g(x), ce qui permet de limiter cette étude au cas plan),

- une définition paramétrique : x(u), y(u), z(u), u entre 0 et 1 ou abscisse curviligne,

- une définition paramétrique vectorielle :

	 ->        ->              ->
	P(u)=fo(u).ao  + ... +fn(u).an

polynômes de Lagrange

Soient N+1 points connus. On cherche à définir une courbe passant exactement par ces points Pi de coordonnées (Xi,Yi), i=0,1,2,...n.

		n
On définit	Y=Pn (x) =	Li (x).Yi
		i=0

Pour que la courbe passe par les points imposés, on peut choisir les polynômes de Lagrange Li tels que :

Li (x) = 1 si x = Xi , Li (x) = 0 si x différent de Xi

Il suffit de prendre :

	(x-X0 )(x-X1 )...(x-Xi-1 )(x-Xi+1 )...(x-Xn )
Li (x) =	--------------------------------------
	(xi -X0 )(xi -X1 )...(xi -Xi-1 )(xi -Xi+1 )...(xi -Xn )

Cette méthode est simple à mettre en oeuvre. Les coefficients sont d'autant plus longs à calculer que l'on a de points. On ne peut pas imposer de condition de tangence, ni influer sur la forme de la courbe entre les points imposées (on peut obtenir des oscillations importantes). Si les nombres de points sont importants, on peut obtenir des produits de Xi-Xj dépassant la capacité de la machine, et prenant beaucoup de temps de calcul. On peut étendre le principe en donnant les points de passage et leurs tangente (polynôme de Hermite). On peut aussi, pour limiter le nombre de points, interpoler la courbe par morceaux. Par Lagrange, la courbe obtenue n'est pas continûment dérivable (rupture de pente entre morceaux) par Hermite seule la dérivée première est continue.

splines

Au lieu de choisir parmi les polynômes de degré n+1, passant par nos n+1 points, un polynôme tel qu'il soit facile à déterminer (Lagrange), choisissons celui qui minimise la fonctionnelle l_q (s) :

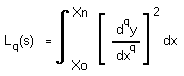
Si q=2, cette fonctionnelle représente l'énergie de déformation en flexion d'une poutre. La minimiser revient à faire passer une fine règle de bois (spline en anglais) par des points imposés. Une autre interprétation consiste à dire que l'on veut minimiser les variations de la tangente à la courbe.

Remarque : la dérivée d'ordre (2q-2) est continue. On peut donc facilement approximer la courbe par morceaux.

la solution est de la forme :

	q-1	n
s(x)=	aj . xj +	Pi (x)
	j=0	i=0

		di <x-xi>+2q-1
avec	Pi (x) =	-------------
		(2q-1)!

et <x-xi>+ = 0 si x < xi , <x-xi>+ = (x-xi ) si x >= xi (partie positive)

Les inconnues du problème sont a_j et d_i .

or pour i=0,1,...,n on a : s(x_i) = y_i

	n
et	di xik = 0 pour k=0,1,...,q-1
	i=0

courbes de Bezier

conditions

on impose à l'origine (u=0) :
- passage en A (f₀ =1 , f_i (0)=0 pour i > 0 )
- la tangente ne dépend que de a₁ (f'i (0)=0 pour i>1 )
- la dérivée seconde ne dépend que de a₁ et a₂ (f''i (0)=0 pour i>2)
- de façon générale, la dérivée kième ne dépend que des k+1 vecteurs a_o à a_k

De plus, le dernier sommet du polygone caractéristique impose le point final de la courbe (u=1), la tangente en ce point ne dépend que du dernier vecteur a_n, etc...

Exemple : pour n=3 : On impose les conditions suivantes :

- passage de la courbe aux deux extrémités du polygone caractéristique : f₁(0)=f₂(0)=f₃(0)=0 ; f₁(1)=f₂(1)=f₃(1)=1

- la tangente en A ne dépend que de a₁ (idem à l'autre extrémité) :

d	d	d	d
--- f2 (0) =	--- f3 (0) =0	--- f1 (1) =	--- f2 (1) =0
du	du	du	du

- la dérivée seconde en A ne dépend que de a₁ et a₂ :

d2	d2
--- f3 (0)=0	--- f1 (1)=0
du2	du2

détermination des polynômes de Bezier

Plaçons nous encore dans le cas de trois points : On a 12 conditions. On peut donc prendre trois fonctions du troisième degré : soit fi (u)=a.u³ + b.u² + c.u + d

la dérivée sera donc f'i (u)=3.a.u² + 2.b.u + c,
et la dérivée seconde f''i (u)=6.a.u + 2.b

d'où : f1 (0)=0 => d=0
f''1 (1)=0 => 6a + 2b = 0 d'où b=-3a
f'1 (1)=0 => 3a-6a+c=0 d'où c=3a
f1 (1)=1 => a+b+c = a+3a-3a = 1 d'où a=1, b=-3, c=3

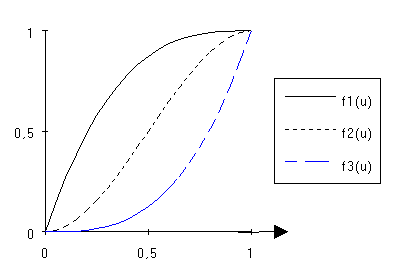
Donc f1(u) = u³ -3.u² + 3.u

de même : f2 (0)=0 => d=0
f'2 (0)=0 => c=0
f2 (1)=1 => a+b=1 d'où b=1-a
f'2 (1)=0 => 3a+2b = 3a+2-2a = 0 d'où a=-2, b=3

donc f2 (u) = -2 u³ + 3.u²

et : f3 (0)=0 => d=0
f'3 (0)=0 => c=0
f''3 (1)=0 => b=0
f3 (1)=1 => a=1 donc f3 (u) = u³

tracé de ces fonctions fim(u) dans le cas m=3 :

P Bezier nous a déterminé le cas général (à l'ordre m) :

^{ou avec}

Cette seconde écriture se traduit facilement de manière informatique, bien que comportant beaucoup de calculs.

forme polynomiale

Plutôt que d'utiliser la formulation vectorielle, on définit le polygone caractéristique par les coordonnées x_i,y_i,z_i de ses sommets. On obtient les coordonnées de tout point de la courbe: Pour accélérer les calculs, on cherchera à stocker dans des tableaux les valeurs intermédiaires réutilisées plusieurs fois pour un tracé. D'autres formulations ont également été développées, on peut les trouver dans divers ouvrages, par exemple dans la collection "Maths et CAO".

intérêt

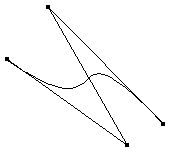
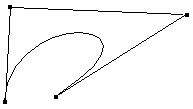
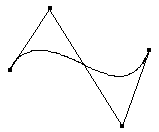
On peut définir une courbe complexe avec assez peu de points caractéristiques. Certes la courbe ne passe pas par ces points, mais avec un peu d'expérience, on "sent" facilement comment déplacer quelques points caractéristiques pour modifier une courbe. Ceci est encore plus intéressant pour des surfaces tridimensionnelles, où les modifications elles aussi se limiteront aux déplacements de quelques points.

exemples

Ces exemples nous montrent la diversité des courbes possibles avec trois ou quatre points :

surfaces

Représenter une surface à l'aide d'un minimum de points est évidement encore plus complexe. De plus, si l'on désire pouvoir modifier facilement une surface, il faut pouvoir le faire en modifiant un minimum de points caractéristiques. On définit en général les surfaces à l'aide de courbes support. Nous nous limitons ici au cas (assez simple) des surfaces de Coons et aborderons les surfaces de Bezier.

Coons

On définit la surface par un réseau de courbes croisées (isoparamétriques). Ceci nous permet de définir des "carreaux", que l'on définit complètement par interpolation surfacique à partir des frontières.

Définissons un carreau et deux paramètres u,v dans [0,1].

la frontière est définie par les quatre équations de courbes suivantes : --> --> --> --> P(u,0) P(u,1) P(0,v) P(1,v)

Déterminons chaque point du carreau par :

--->	-->	-->
P(u,v) =	P(u,0).f0 (v)+	P(u,1).f1 (v)
	-->	-->
	+ P(0,v).f0 (u) +	P(1,v).f1 (u)
	-->	-->
	- P(0,0).f0 (u).f0 (v) -	P(0,1).f0 (u).f1 (v)
	-->	-->
	- P(1,0).f1 (u).f0 (v) -	P(1,1).f1 (u).f1 (v)

Les conditions nécessaires au passage de la surface par les frontières sont : f₀ (0)=1, f₀(1)=0, f₁(0)=0, f₁(1)=1. On peut choisir n'importe quelle solution, par exemple f0(t)=1-t, f₁(t)=t, ce qui permet de définir une surface limitée par les frontières définies. Mais pour que le principe ait une quelconque utilité, il faut au minimum une continuité en tangence entre les carreaux. Coons propose pour cela :
f₀ (t) = 2t³ - 3t² + 1
f₁ (t) = -2t³ + 3t²

De même, pour obtenir une continuité en courbure, on pourra prendre (à condition évidement d'avoir des courbes isoparametriques continues en courbure) :
f₀ (t) = -6t⁵ + 15t⁴ - 10t³ + 1
f₁ (t) = 6t⁵ - 15t⁴ + 10t³

surfaces de Bezier

On utilise un réseau croisé de polygones de Bezier. Toutes les courbes "parallèles" doivent donc être définies par le même nombre de points caractéristiques. Nous supposerons disposer de m+1 courbes d'ordre n, la courbe i étant définie par :

	->	->	->	->
	Pi(u)=	OAi +f1n (u)	ai1 + ... +fnn (u)	ain		(i dans [0,m])

Les points A_i forment eux aussi un polygone caractéristique. On note a_i le vecteur A_i-1A_i.

Les points caractéristiques de même "niveau" forment des polygones caractéristiques "perpendiculaires". Mais les courbes définies par ces polygones ne se croisent pas nécessairement (puisqu'elles ne passent pas par les points caractéristiques). La surface elle non plus ne passe pas par ces courbes, mais elle est bordée par les quatre courbes frontières.

-->

-->

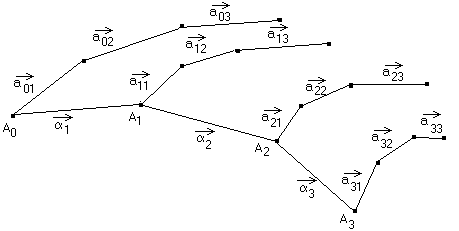
m

->

n

->

m

n

->

->

P(u,v) =

OA0

+

ai

fim(u)

+

a0j

fjn(v)

+

(aij-

ai-1,j)

fim(u) fjn(v)

i=1

j=1

i=1

j=1

Je ne serai pas plus précis ici, de nombreux ouvrages traitant de ce problème, en particulier le livre de P. Bezier, dans la collection Maths et C.A.O. chez Hermes.