.
Cette seconde méthode évite de calculer les
coefficients de la droite, c'est celle que je vous propose
d'utiliser.
Aujourd'hui, nous allons mettre en place quelques outils pour déterminer l'enveloppe d'un ensemble de points (dans le plan). Le nombre de points est spécifié dans une variable entière «nbpts». Ces points sont définis par leurs deux coordonnées réelles x et y, dans deux tableaux (le point n°i a pour coordonnées x(i),y(i), iÎ[1,nbpt] ). Supposons qu'il n'y aura jamais plus de 100 points.
Nous allons rechercher la courbe enveloppe de ces points. C'est un polygone convexe, que l'on définira par ses sommets.
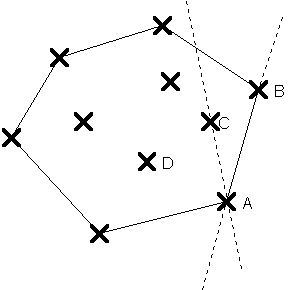
Il existe un plusieurs méthodes pour déterminer le polygone convexe englobant tous les points. Je vous propose d'utiliser la suivante : on analyse tous les couples de points possibles. Pour chacun de ces couples, on détermine la droite passant par ces deux points, et l'on teste la position de tous les autres points. S'ils sont tous du même côté, et uniquement dans ce cas, le couple forme un segment de la frontière.
Par exemple, le segment AB fait partie de l'enveloppe car tous les autres points sont du même côté de la droite AB, mais le segment AC n'en fait pas partie car B et D sont de part et d'autre de la droite AC.
Bien que vous sachiez tous comment vérifier de quel côté d'une droite est un point, je vais vous en rappeler deux méthodes (saviez vous que l'équation d'une droite n'est pas y=ax+b, à cause des horizontales ?) :
a) Il faut mettre l'équation de la droite sous la forme ax+by+c=0. Alors tout point (x,y) appartient à la droite si ax+by+c=0, tout point situé d'un côte (demi-plan) vérifie ax+by+c<0, alors que les points de l'autre demi-plan vérifient ax+by+c>0.
b) D et C sont du même côté
de AB si
.
Cette seconde méthode évite de calculer les
coefficients de la droite, c'est celle que je vous propose
d'utiliser.
Rappel : deux nombres sont de même signe si leur produit est positif.
Question 1 : Ecrivez un sous-programme qui demande le nombre de points et leurs coordonnées. Il s'appellera «saisie». Ecrivez également un sous-programme «affichage» qui sache afficher ces données, et un programme qui permette de tester s'ils fonctionnent. Les tableaux X,Y ainsi que le nombre de points peuvent être dans une zone commune, et déclarés grâce à un include, cela simplifiera la suite du TP.
Question 2 : Ecrivez une fonction appelée SignCote qui :
reçoit en entrée trois entiers : les indices, dans les tableaux x et y, de deux points (A et B) définissant un segment, et d'un troisième (C) dont on veut connaître le côté par rapport à la droite AB (ainsi que les autres données dont vous aurez besoin)
retourne la valeur du produit vectoriel
.
Attention : «reçoit» signifie pour moi que ces nombres sont calculés ou saisis autre part, et transmis en argument à la fonction !
Question 3 : Ecrivez une fonction appelée frontiere qui reçoit en argument d'entrée deux entiers : les indices, dans les tableaux x et y, de deux points (A et B) définissant un segment; et retourne un logical valant .TRUE. si tous les autres points sont du même côté du segment AB , et valant .FALSE. dans le cas contraire. Ecrivez un programme principal utilisant ces fonctions et affichant tous les segments appartenant à la frontière (les indices et les coordonnées des points), dans n'importe quel ordre (vous essayerez toutes les segments possibles).
Question 4 : On aimerait maintenant déterminer la suite ordonnée des points formant l'enveloppe. Pour cela, écrivez un sous-programme ou une fonction qui recherche le point le plus bas (coordonnée y minimale, s'il y en a plusieurs celui le plus à gauche). A partir de ce point trouvez un segment frontière passant par ce point, puis partez de l'autre extrémité du segment, jusqu'à faire tout le tour. Prenez garde de ne pas «rebrousser chemin». Faites le programme complet, de la saisie des données à l'affichage des points de la frontière. J'aimerais avoir la suite des indices des points de la frontière dans un tableau, mais juste les afficher sera déjà pas mal.
Comme la fois précédente, transférez votre programme (bien nommé, sans espace).
La correction est disponible ici : source et fichier inclus, ou les deux en pdf.
| sujet TP1 | sujet TP2 | sujet TP3 | sujet TP4 | retour sommaire TP | cours Fortran | P. Trau |