

Les composantes de l'arbre seront donc soit des opérateurs (noeuds), soit des opérandes (feuilles). Nous allons choisir les déclarations suivantes :
typedef float type_feuille;
typedef struct s_noeud_2
{char op_c;
struct s_comp*fils1;
struct s_comp*fils2;
}type_noeud_2;
typedef struct s_noeud_1
{char op_c;
struct s_comp*fils;
}type_noeud_1;
typedef struct s_comp
{int arite;
union
{type_noeud_2 n2;
type_noeud_1 n1;
type_feuille f;
}val;
}composante;
typedef composante *lien;
Nous prévoyons donc deux types de noeuds : à arité 1 (avec
un fils) ou à arité 2 (deux fils). On aurait pu utiliser un seul
type (à arité 2) en mettant NULL dans le second fils en cas
d'arité 1. Une feuille par contre ne contient aucun lien. Une composante
de l'arbre contiendra donc un indicateur de son type (ici l'arité) et,
suivant ce type, soit une feuille, soit un noeud (d'arité 1 ou 2). Nous
allons écrire une fonction créant un tel arbre (à partir
d'une chaîne de caractères préalablement saisie, contenant
l'expression en notation polonaise préfixée
par exemple) :
{
lien x;
char c;
while(**deb==' '||**deb==',') (*deb)++;
if(**deb==0) /* on est arrivé en fin de chaîne */
{puts("erreur : il doit manquer des opérandes");
return(NULL);}
x=(composante*)malloc(sizeof(composante));
if(isdigit(**deb))
{
x->arite=0;
sscanf(*deb,"%f",&(x->val.f));
while(isdigit(**deb)||**deb=='.') (*deb)++;
}
else
{
c=toupper(*((*deb)++));
if(c=='*'||c=='/'||c=='+'||c=='-')
{
x->arite=2;
x->val.n2.op_c=c;
x->val.n2.fils1=saisie_prefixe(deb);
x->val.n2.fils2=saisie_prefixe(deb);
}
else if(c=='C'||c=='S')
{
x->arite=1;
x->val.n1.op_c=c;
x->val.n1.fils=saisie_prefixe(deb);
}
else printf("erreur, '%c'n'est pas un opérateur prévu\n",c);
}
return(x);
}
On peut remarquer que cette fonction est récursive.
La création de l'arbre à partir d'une expression postfixée
est similaire (scruter la chaîne dans l'autre sens par exemple), à
partir d'une expression infixée
c'est un peu plus dur, surtout si l'on ne veut pas imposer d'entrer toutes les
parenthèses, par exemple 1+2+3 au lieu de (1+(2+3)).L'utilisation d'un tel arbre devient maintenant très simple. On utilisera la récursivité. Pour évaluer l'expression, si c'est une feuille unique la valeur est celle de la feuille, si c'est un noeud, la valeur est obtenue en effectuant l'opération correspondante, après évaluation (récurrente, donc soit directement la valeur si feuille soit nouveau calcul) de ses fils :
float eval(lien x)
{
float r1,r2;
if(x->arite==0) return(x->val.f);
else if (x->arite==1)
{
if (x->val.n1.op_c=='C')
return(cos(eval(x->val.n1.fils)));
else if (x->val.n1.op_c=='S')
return(sin(eval(x->val.n1.fils)));
}
else
{
r1=eval(x->val.n2.fils1);
r2=eval(x->val.n2.fils2);
switch (x->val.n2.op_c)
{
case '+':return(r1+r2);
case '-':return(r1-r2);
case '*':return(r1*r2);
case '/':return(r1/r2);
}
}
/* si aucun return n'a été effectué jusqu'ici*/
puts("erreur (code opératoire inconnu par exemple)");
return(0);
}
Le parcours
des arbres (c'est à dire le passage par tous les noeuds et feuilles) se
fait d'habitude de manière récursive. On doit évidement
parcourir l'arbre pour afficher son contenu. On peut utiliser dans le cas des
arbres binaires trois possibilités de parcours : afficher la valeur du
noeud puis récursivement de ses deux fils, afficher le premier fils, la
valeur du noeud, puis le second fils, ou afficher les deux fils avant la valeur
du noeud. On obtient dans notre cas directement les notations
préfixé, infixée et postfixée (avec un petit
travail supplémentaire pour la gestion des parenthèses en
notation infixée, qu'on aurait pu simplifier si l'on avait
accepté des parenthèses surabondantes) :
void affiche_prefixe(lien x)
{
switch(x->arite)
{
case 0:printf("%6.1f ",x->val.f);break;
case 1:printf(" %C ",x->val.n1.op_c);
affiche_prefixe(x->val.n1.fils);
break;
case 2:printf(" %c ",x->val.n2.op_c);
affiche_prefixe(x->val.n2.fils1);
affiche_prefixe(x->val.n2.fils2);
}
}
void affiche_postfixe(lien x)
{
switch(x->arite)
{
case 0:printf("%6.1f ",x->val.f);break;
case 1:affiche_postfixe(x->val.n1.fils);
printf(" %C ",x->val.n1.op_c);
break;
case 2:affiche_postfixe(x->val.n2.fils1);
affiche_postfixe(x->val.n2.fils2);
printf(" %c ",x->val.n2.op_c);
}
}
void affiche_infixe(lien x)
{
switch(x->arite)
{
case 0:printf("%6.1f ",x->val.f);break;
case 1:printf(" %C( ",x->val.n1.op_c);
affiche_infixe(x->val.n1.fils);
putch(')');
break;
case 2:if(x->val.n2.fils1->arite!=0)putch('(');
affiche_infixe(x->val.n2.fils1);
if(x->val.n2.fils1->arite!=0)putch(')');
printf(" %c ",x->val.n2.op_c);
if(x->val.n2.fils2->arite!=0)putch('(');
affiche_infixe(x->val.n2.fils2);
if(x->val.n2.fils2->arite!=0)putch(')');
}
}
Notre exemple est un peu plus complexe que dans véritable arbre
binaire, puisque nous acceptions également des noeuds à un seul
fils.
typedef struct s_noeud *lien;
typedef struct s_noeud
{char *nom;
lien fils1;
lien fils2;
}type_noeud;
Il vaut mieux ne pas prévoir de type spécifique pour les
feuilles, l'arbre étant géré de manière
évolutive (une feuille sera donc un noeud avec ses deux fils valant le
pointeur NULL). Le nom contenu dans chaque noeud aurait pu être un
tableau statique de caractères, mais pour optimiser le coût
mémoire, nous utiliserons un tableau dynamique. Donc, pour allouer la
mémoire d'un nouveau noeud, deux malloc
seront nécessaires : un pour le noeud lui-même, et un pour le nom
qui lui est associé. Ecrivons une fonction de création d'un noeud
(on lui transmet le nom associé, elle retourne l'adresse allouée):
lien cree_feuille(char *nouv_nom)
{
lien x;
int taille;
x=(lien)malloc(sizeof(type_noeud));
taille=strlen(nouv_nom)+1; /* compter le \0 */
x->nom=(char*)malloc(taille);
strcpy(x->nom,nouv_nom);
x->fils1=NULL;
x->fils2=NULL;
return(x);
}
Supposons entrer dans l'ordre : Jean, Bernard, Lucie, Anne, Jacques,
Laurent, Maud, Luc, Julie, Elsa. Si vous créez progressivement l'arbre,
vous pourrez voir que toute nouvelle valeur trouve toujours sa place, les
feuilles se transformant petit à petit en noeuds, au fur et à
mesure de l'augmentation de la taille de l'arbre.

La fonction effectuant la saisie et la création de cet arbre devra donc, après la saisie du nouveau nom à insérer, rechercher sa position définitive. Cette recherche sera récursive: sur un noeud donné, si le nouveau nom est plus petit, rechercher dans la descendance du fils1, sinon rechercher dans la descendance du fils2. La recherche s'arrête quand on arrive à un pointeur NULL (qui sera remplacé par l'adresse du nouveau noeud). En cas d'égalité, si l'on désire une création stable, un nouveau nom sera placé derrière ceux déjà existants. :
void insert_feuille(lien racine, lien x)
{
while(racine!=NULL) /* ou boucle infinie */
{
if(strcmp(x->nom,racine->nom)<0)
if(racine->fils1==NULL){racine->fils1=x;return;}
else racine=racine->fils1;
else
if(racine->fils2==NULL){racine->fils2=x;return;}
else racine=racine->fils2;
}
}
lien saisie(void)
{
lien racine=NULL;
char txt[100];
do
{
printf("entrez un nouveau nom, @@@ pour finir : ");
gets(txt);
if(strcmp(txt,"@@@"))
if(racine==NULL)racine=cree_feuille(txt);
else insert_feuille(racine,cree_feuille(txt));
}
while(strcmp(txt,"@@@"));
return(racine);
}
On remarque l'efficacité de cette méthode : aucun
déplacement d'élément, le tri se fait par insertion, mais
avec recherche optimisée (du type dichotomie : l'espace de recherche est
réduit à chaque test). Pour N insertions, on fait donc N
recherches donc N*P lectures de composantes (P profondeur de l'arbre).Une fois l'arbre créé, on peut afficher la liste triée par ordre alphabétique par un simple parcours infixé (arbr_nom):
void affiche(lien x)
{
if(x!=NULL)
{
affiche(x->fils1);
printf("%s, ",x->nom);
affiche(x->fils2);
}
}
L'utilisation d'un arbre binaire
pour une liste triée permet donc une programmation relativement
aisée, des algorithmes rapides, mais moyennant un peu de place
mémoire supplémentaire. L'arbre va posséder
simultanément tous les avantages des autres structures de données:

En fait, plutôt que de créer cette liste hors des noeuds, le plus simple (et qui utilise autant de mémoire) est d'associer à chaque noeud l'adresse de son fils aîné, et de son frère cadet. Accéder à tous les fils revient donc à accéder au fils aîné puis à tous ses frères:
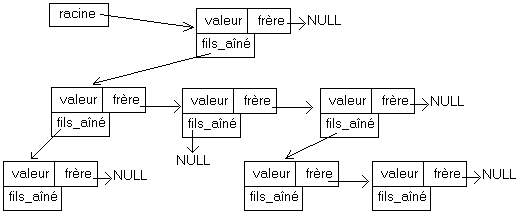
On peut remarquer qu'un tel arbre est un arbre binaire: chaque noeud possède deux liens. On peut donc traiter tout arbre sous forme d'un arbre binaire.
Une autre amélioration possible d'un arbre est de permettre un accès toujours séquentiel mais bidirectionnel : pour un arbre binaire, chaque noeud possède en plus l'adresse de son père, pour un arbre généralisé ceci revient à ce que chaque frère connaît son aîné, l'aîné connaissant leur père commun. Cet accès bidirectionnel est coûteux en mémoire, mais complique également les modifications (plus de liens à gérer), pour par contre accélérer les parcours dans l'arbre. On ne prévoira cette amélioration que lorsque l'on utilise de fréquentes remontées (l'utilisation d'algorithmes récursifs ne nécessite en général pas ces liens, le fait de quitter une fonction appelée pour gérer un fils fait automatiquement retrouver le père).