
typedef float type_val;
typedef struct scomp {type_val val; struct scomp *suiv;} type_comp;
typedef type_comp *adr_comp;
Nous représenterons les composantes des listes (de type
type_comp) ainsi :

Supposons disposer de la liste ci-dessous en mémoire (nous verrons plus loin comment la créer en mémoire). La variable prem, de type adr_comp (donc pointeur sur une composante) contient l'adresse de la première composante. Le champ suiv de la dernière composante contient la valeur NULL, donc ne pointe sur rien.

Pour simplifier les algorithmes, on peut mettre d'office une composante particulière en début et fin de liste (appelée sentinelle). Ceci évite de devoir traiter de manière particulière le premier et dernier élément de la liste, puisque chaque composante utile possède toujours un précédent et un suivant. Cette méthode prend un peu plus de mémoire (négligeable en % pour de longues listes) et évite des tests systématiques dans le boucles, alors qu'ils ne servent que pour les extrémités (d'où gain de temps appréciable, toujours en cas de longues listes). Une autre méthode pour repérer le dernier élément est de le faire pointer sur lui-même. Nous utiliserons dans la suite des listes sans sentinelle, le dernier élément pointant sur NULL.
L'appel de : affiche_lst(prem) affichera à l'écran le contenu de la liste :
void affiche_lst(adr_comp l)
{
while(l!=NULL)
{
printf("%6.1f ",l->val);
l=l->suiv;
}
printf("\n");
}
l pointe sur la première composante. On affiche la valeur
pointée par l puis on fait pointer l sur son suivant. On
répète le processus jusqu'en fin de liste (lorsque l'on pointe
sur NULL). La variable l doit être locale (donc passée par valeur)
pour ne pas modifier le contenu de prem, et donc perdre l'adresse du
début de la liste, ce qui empêcherait tout accès
ultérieur à la liste.Comme pour les chaînes de caractères, plutôt que de gérer un variable entière indiquant toujours la longueur actuelle de la liste, c'est la spécificité du dernier élément (ici, le champ suiv contient NULL) qui permet de préciser que l'on est en fin de liste. Pour connaître la longueur d'une liste, on utilisera :
int longueur_lst(adr_comp l)
{
int n=0;
while(l!=NULL)
{
l=l->suiv;
n++;
}
return(n);
}
Les listes ont l'avantage d'être réellement dynamiques,
c'est à dire que l'on peut à loisir les rallonger ou les
raccourcir, avec pour seule limite la mémoire disponible (ou la taille
du super-tableau). Par exemple pour insérer une nouvelle composante en
début de liste, on utilisera :
void insert_premier(adr_comp *prem,type_val val)
{
adr_comp nouv;
nouv=(adr_comp)malloc(sizeof(type_comp));
nouv->val=val;
nouv->suiv=*prem;
*prem=nouv;
}
En insérant la valeur 5 à notre exemple
précédent, on obtient la liste :

La variable prem a dû être passée par adresse, pour que l'on récupère bien l'adresse de la nouvelle première composante (appel : insert_premier(&prem,5)). En fait le schéma ci-dessus n'est qu'une représentation abstraite de la liste (chaque composante pointe sur la suivante), alors que les composantes sont physiquement placées différemment en mémoire. Dans le meilleur des cas, la nouvelle composante créée a été placée juste derrière celles déjà existantes (premier emplacement libre). Un schéma plus proche de la réalité serait donc :
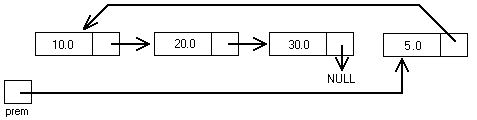
Ces deux schémas sont équivalents (les liens partent des mêmes cases, et pointent sur les mêmes cases), seule la disposition des cases diffère. En fait ceci nous montre bien que la disposition réelle en mémoire ne nous intéresse pas (jamais la valeur effective de l'adresse contenue dans un pointeur ne nous intéressera). Dans nos schémas, nous choisirons donc une disposition des composantes correspondant plus au problème traité qu'à la disposition réelle en mémoire (par exemple dans le schéma suivant, on utilise une représentation bidimensionnelle, alors que la mémoire n'est qu'unidimensionnelle).
Le second avantage des listes est que l'insertion
d'une composante au milieu d'une liste ne nécessite que la modification
des liens avec l'élément précédent et le suivant,
le temps nécessaire sera donc indépendant de la longueur de la
liste. Supposons disposer d'une variable X de type adr_comp, pointant
sur la composante de valeur 10. L'appel de insert_après(X,15)
donnera le résultat suivant :

void insert_après(adr_comp prec,type_val val)
{
adr_comp nouv;
nouv=(adr_comp)malloc(sizeof(type_comp));
nouv->val=val;
nouv->suiv=prec->suiv;
prec->suiv=nouv;
}
Cette fonction permet l'insertion en tout endroit de la liste, sauf en
première position (qui n'a pas de précédent dans notre cas
puisque sans sentinelle), il faut traiter spécifiquement le premier de
la liste (voir plus haut). L'insertion nécessite la connaissance de
l'adresse du précédent et du suivant. Les composantes ne
comportant que des liens vers l'élément suivant, il faut
nécessairement donner à la fonction insert_après l'adresse
du précédent, alors que d'habitude on préfère
donner l'élément devant lequel on veut faire l'insertion
(tableaux par exemple). Ceci nous montre le principal problème des
listes : l'accès est séquentiel.
On devra, pour chercher la composante précédente, parcourir toute
la liste depuis son début (on donne l'adresse du début de la
liste et de l'élément dont on cherche le précédent):
adr_comp rech_prec(adr_comp prem, adr_comp suiv)
/* rend l'adresse, NULL si non trouvé */
{
while(prem->suiv!=suiv && prem!=NULL)
prem=prem->suiv;
return(prem);
}
Une autre solution, si l'on a fréquemment besoin de parcourir
la liste vers l'avant et vers l'arrière, est de stocker dans chaque
composante l'adresse du suivant et celle du précédent. Ceci
nécessite plus de place en mémoire et ralentit un peu les
manipulations de base (il y a plus de liens à mettre à jour).
Mais même dans ce cas, l'accès reste séquentiel. Ceci
empêche d'utiliser un certain nombre d'algorithmes utilisant
l'accès direct (la dichotomie par exemple). Pour trouver l'adresse du
Nième élément d'une liste il faudra utiliser (on suppose
numéroter 0 le premier) :
adr_comp rech_ind(adr_comp l, int i)
/* rend l'adresse du (i+1)ième, NULL si liste trop courte */
{
int j;
for(j=0;j<i && l!=NULL;j++) l=l->suiv;
return(l);
}
La recherche d'un élément, même si la liste est
triée, se fera donc toujours séquentiellement :
adr_comp rech_val(adr_comp l, type_val v)
/* rend l'adresse, NULL si non trouvé */
{
while(l!=NULL && l->val!=v) l=l->suiv;
return(l);
}
Pour créer une liste, la solution la plus simple consiste
à boucler sur un appel de la fonction insert_premier, mais les
éléments seront stockés dans l'ordre inverse de leur
introduction (le dernier saisi sera placé en premier). Pour une
création de liste dans l'ordre, on fera :
adr_comp saisie_lst(void)
{
adr_comp prem=NULL,prec,actu; /* premier, précédent, actuel*/
type_val v;
int err;
do
{
printf("entrez votre prochaine valeur, un caractère pour finir :");
err=scanf("%f",&v);
if(err<=0)break; /*scanf rend le nombre de variables lues sans erreur*/
actu=(adr_comp)malloc(sizeof(type_comp));
actu->val=v;
if(prem==NULL)prem=actu; else prec->suiv=actu;
prec=actu;
}
while(1);
actu->suiv=NULL;
return(prem);
}
Cette fonction crée la liste en mémoire, effectue la saisie et
retourne l'adresse du début de la liste.Il nous reste à traiter les suppressions dans une liste. Il faut ici encore préciser l'élément précédent celui à supprimer, et traiter de manière particulière le début de la liste :
void suppr_suivant(adr_comp prec)
{
adr_comp a_virer;
if(prec==NULL || prec->suiv==NULL)
{puts("rien à supprimer");return;}
a_virer=prec->suiv;
prec->suiv=a_virer->suiv;
free(a_virer);
}
void suppr_premier(adr_comp *prem)
{
adr_comp a_virer;
if(*prem==NULL) {puts("rien à supprimer");return;}
a_virer=*prem;
*prem=(*prem)->suiv;
free(a_virer);
}
La suppression
complète d'une liste permet de récupérer la place en
mémoire. Cette opération n'est pas nécessaire en fin de
programme, le fait de quitter un programme remet la mémoire dans son
état initial et libère donc automatiquement toutes les
mémoires allouées dynamiquement :
{
adr_comp deuxieme;
while(prem!=NULL)
{
deuxieme=prem->suiv;
free(prem);
prem=deuxieme;
}
}
Il n'était à priori pas obligatoire d'utiliser la
variable deuxième car la libération par free
n'efface pas les mémoires, le suivant est donc encore disponible
après free et avant tout nouveau malloc. Néanmoins cette
écriture est plus sure, ne gérant pas la mémoire nous
même (sauf si méthode du super-tableau), en particulier en cas de
multitâche, d'interruption matérielle...On trouvera un exemple utilisant ces fonctions dans test_lst.c (disquette d'accompagnement)
void tri_bulle_lst(adr_comp *prem)
/* le premier ne sera peut-être plus le même donc passage par adresse */
{
int ok;
adr_comp prec,actu,suiv;
do
{
ok=1; /* vrai */
prec=NULL;
actu=*prem;
suiv=actu->suiv;
while(suiv!=NULL)
{
if(actu->val > suiv->val)
{
ok=0;
if(prec!=NULL) prec->suiv=suiv; else *prem=suiv;
actu->suiv=suiv->suiv;
suiv->suiv=actu;
}
prec=actu;
actu=suiv;
suiv=actu->suiv;
}
}
while(!ok);
}
En utilisant prec->suiv et
prec->suiv->suiv, on pouvait éviter d'utiliser les
variables actu et suiv. Le temps d'accès aux variables
aurait été un peu plus long mais on supprimait deux des trois
affectations situées en fin de boucle.
void tri_insertion_lst(adr_comp *prem)
{
/*position testée, précédent,dernier plus petit*/
adr_comp pt,prec,dpp;
for(prec=*prem,pt=(*prem)->suiv;pt!=NULL;prec=pt,pt=pt->suiv)
if(prec->val>pt->val) /*inutile de chercher si en bonne
position */
{
prec->suiv=pt->suiv;
if((*prem)->val > pt->val) /*cas particulier du premier*/
{
pt->suiv=*prem;
*prem=pt;
}
else
{
dpp=*prem;
while(dpp->suiv->val <= pt->val)dpp=dpp->suiv;
/* on est sur d'en trouver un, vu les tests effectués plus haut */
pt->suiv=dpp->suiv;
dpp->suiv=pt;
}
}
}
Ici également, on aurait pu tenter d'éviter
l'utilisation des deux variables prec et pt puisque pt est le suivant de prec,
mais les échanges auraient alors nécessité une variable
tampon. Cette version du tri est stable
(le nouveau est inséré derrière les valeurs
égales), mais ceci ralentit un peu la recherche de la position
définitive d'une valeur en cas de nombreuses valeurs égales (si
la stabilité n'est pas nécessaire, il suffit d'arrêter la
recherche au premier élément supérieur ou égal).
Dans tous les cas, on fera au maximum N échanges (aucun en bonne
position), en moyenne N/2 pour les fichiers mélangés. Dans la cas
d'un fichier mélangé, le nombre de boucles internes est de
N(N-1)/2 en moyenne. Dans le cas d'un fichier presque trié, dans le cas
de quelques éléments (en nombre P) pas du tout à leur
place, ce tri est très efficace : P échanges, (P+2)*N/2 boucles
internes, donc on devient linéaire en N. Par contre dans le cas de
nombreux éléments pas tout à fait à leur place
(à la distance D), il l'est moins que le tri bulle, la recherche de la
position exacte se faisant à partir du début de la liste (proche
de N2 : (N-D)(N-1) boucles internes). Dans ce cas, si l'on peut
également disposer d'un chaînage arrière, on fera la
recherche à partir de la position actuelle, ce qui rendra le tri
très efficace également dans ce cas : D(N-1) boucles internes
donc linéaire en N. Sinon, on peut mémoriser la position du
Dième précédent, le comparer à la valeur à
insérer et donc dans la majorité des cas (si D bien choisi)
rechercher derrière lui, dans les quelques cas où il faut
l'insérer devant lui, on effectue une recherche depuis le début.
void tri_selection_lst(adr_comp *prem)
{
type_comp faux_debut;
adr_comp pdpd,pdpp,i;
faux_debut.suiv=*prem;
for(pdpd=&faux_debut;pdpd->suiv!=NULL;pdpd=pdpd->suiv)
{
/*recherche du plus petit (du moins son précédent)*/
pdpp=pdpd; /*le plus petit est pour l'instant l'actuel, on va tester les suivants*/
for(i=pdpd->suiv;i->suiv!=NULL;i=i->suiv)
if(i->suiv->val < pdpp->suiv->val)pdpp=i;
/* échange (si beaucoup d'éléments
déjà en place, rajouter un test pour ne pas échanger
inutilement) */
i=pdpp->suiv;
pdpp->suiv=i->suiv;
i->suiv=pdpd->suiv;
pdpd->suiv=i;
}
*prem=faux_debut.suiv; /* retourner le bon premier */
}
pdpd représente le Précédent De la Place
Définitive (boucle principale : de place définitive valant *prem
jusqu'à fin de la liste), pdpp représente le
Précédent Du Plus Petit (de la suite de la liste, pas encore
traitée). On a dans cette implantation évité les variables
pour la place définitive et le plus petit, ceux-ci étant les
suivants des variables précisées ci-dessus. Ceci nuit à la
clarté mais améliore l'efficacité. On pouvait
améliorer la clarté (définir les "variables" pd et pp)
sans nuire à l'efficacité (ne pas devoir les remplacer par leur
suivant en fin de boucle) par des #define
:#define pd pdpd->suiv #define pp pdpp->suivPour limiter la portée de ces substitutions à cette fonction, il suffit de déclarer juste derrière la fin de la fonction :
#undef pd #undef ppDe plus, afin d'éviter de tester partout le cas particulier du premier de la liste, on a choisi d'ajouter un élément en début de liste (faux_début), pointant sur le premier de la liste. Dans ce cas, tous les éléments y compris le premier ont un précédent. Le gain est donc appréciable (en temps car moins de tests et en taille du code source), pour un coût limité à une variable locale supplémentaire.
Pour le tri rapide, le nombre de boucles internes est de l'ordre de Nlog(N) (N sur toute la liste, puis deux fois N/2 sur les deux moitiés.... donc N*P, P étant la profondeur de récursivité, qui est de log(N)). Par contre les échanges sont plus nombreux que les autres tris (en moyenne une boucle interne sur deux pour un fichier mélangé). Pour transposer l'implantation détaillée pour les tableaux, il faut disposer d'une liste à chaînage avant et arrière, mais il est facile de n'utiliser que le chaînage avant : l'algorithme devient donc :